正则化(regularization),是指在线性代数理论中,不适定问题通常是由一组线性代数方程定义的,而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。(百度百科:) 主要解决的问题:
正则化就是对最小化经验误差函数上加约束,这样的约束可以解释为先验知识(正则化参数等价于对参数引入先验分布)。约束有引导作用,在优化误差函数的时候倾向于选择满足约束的梯度减少的方向,使最终的解倾向于符合先验知识(如一般的l-norm先验,表示原问题更可能是比较简单的,这样的优化倾向于产生参数值量级小的解,一般对应于稀疏参数的平滑解)。
同时,正则化解决了逆问题的不适定性,产生的解是存在,唯一同时也依赖于数据的,噪声对不适定的影响就弱,解就不会过拟合,而且如果先验(正则化)合适,则解就倾向于是符合真解(更不会过拟合了),即使训练集中彼此间不相关的样本数很少。
总之:
- 正则化的目的:防止过拟合。
- 正则化的本质:约束(限制)要优化的参数。
因此,引入正则化项,也就是\(L_p\)范数。
具体有:
- L0范数:非零元素的个数,稀疏解,但不连续不可导。
- L1范数:绝对值之和,稀疏解,连续但部分可导(与坐标轴相交的部分)。
- \(L_p\)范数:\((\sum\limits_{\rm{i}} {x_i^p}) {^{\frac{1}{p}}}\)
- \(L\infty\)范数:\({\left\| x \right\|_\infty } = \max (| x_i |)\)
考虑线性模型,损失函数为平方损失:
\[f(x)=w^Tx\] 则优化目标为: \[\min _w \sum_{i=1}^m (y_i-w^Tx_i)^2\]
引入正则化项则变成: \[\min _w \sum_{i=1}^m (y_i-w^Tx_i)^2 + \lambda||w||_p^p\]
L2的叫岭回归,可以直接求解,因为逆存在。
L1的叫LASSO,可以使用近端梯度下降(PGD)求解,泰勒二阶展开。
那么,为什么L1更容易获得稀疏解呢:
首先我们看图:
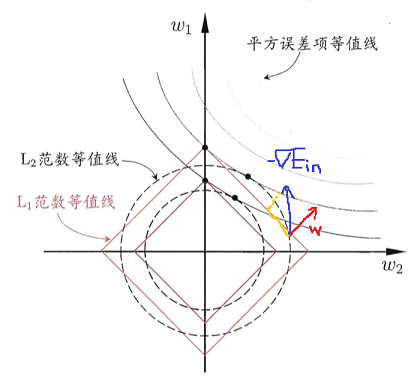
最优解的位置在\(-\nabla {E_{in}}\)和w平行的位置。
而在L1范数的坐标限中,\(\nabla {E_{in}}\)和w往往不共线,它还有一个下降的分量拉扯它到坐标轴的交点上。
至此,正则化讲解完毕。
