正则化就是控制模型复杂度的一种办法

解释1：PAC学习泛化界解释

奥坎姆剃刀理论：优先选择拟合数据的最简单的假设。 简单的模型才是最好的。

解释2：偏差方差分解

过拟合发生在模型完美拟合训练数据，对新的数据效果不好。 正则化通过简化模型降低方差，会增加偏差。

解释3：贝叶斯先验

先验知识在数据少的时候，可以防止过拟合

通俗的解释：

过拟合的时候，拟合函数的系数往往非常大，需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。 而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

L2权重衰减

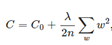
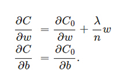
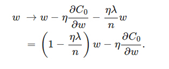
1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。

L1正则

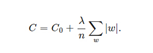
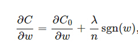
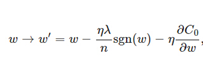
η * λ * sgn(w)/n这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大——因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。可以规定sgn(0)=0。