线性模型是机器学习最基础的模型,但却十分强大,很多复杂模型都是线性模型的变体。
首先,最基础的线性模型为\(h=w^Tx+b\)。
根据数据算出一个分数(score),这就是回归模型,再加上一个阈值判断,如
\[ {\rm{h}} = \theta ({w^T}x) = \left\{ {\begin{array}{*{20}{c}} {1,{w^T}x \ge 0.5}\\ {0,{w^T}x < 0.5} \end{array}} \right. \]
接下来我们分析不同的模型(主要从损失函数分析):
回归模型
线性回归:
损失函数采用平方损失
\[ L = \sum\limits_{i = 1}^N {({y_i} - {w^T}{x_i})} \] 求解,可以采用梯度下降法。写成向量的形式:
\[ L = (y-Xw)^T(y-Xw) \]
对\(w\)求导:
\[ \frac{\partial L}{\partial w} = 2{X^T}(Xw - y) \]
当\(X^TX\)为满秩矩阵或正定矩阵,也就是可逆,得:
\[ w^*=(X^TX)^{-1}X^Ty \]
最终的线性模型为:
\[ g = (X^TX)^{-1}X^Tyx \]
分类模型
如何分类?直接讲,如果概率大于0.5,我们就认为他是1类,否则就是0类。
感知机
更多的感知机算法,详情见: http://wuqiansheng.xyz/2018/04/09/感知机算法/。
这里主要从损失函数方向推导:空间一个点到超平面的距离为:
\[ \frac{1}{||w||}|w^Tx_i+b| \]对于误分类的点\((x_i,y_i)\):
什么叫误分类呢,感知机的阈值定为0,其实0.5,0都一样,只不过是在\(b\)上加个偏移。
误分就是:
\[ -y_i(w^Tx_i+b)>0 \]那么损失函数为:
\[ L=\sum_{i}^{N} \max(0, y_i(w^Tx_i+b)) \]
换成另外一种形式,极小化:
\[ L=-\sum_{x_i \in M}{y_i(w^Tx_i+b)} \]采用梯度下降求解。 \[ w = w+\eta y_ix_i \\ b = b+\eta y_i \] \(\eta\)为更新步长,又称学习率。
考虑它的对偶模型为:
考虑最终的\(w,b\)是修改n次后的增量,也就是: \[ w=\sum_{i=1}^{N}\alpha_iy_ix_i \\ b=\sum_{i=1}^{N}\alpha_iy_i \\ \] 其中\(\alpha_i=n_i\eta\)。
最终的\(h\)如下: \[ h=\sum_{i=1}^{N}\alpha_iy_ix_i\cdot x+b \]
逻辑回归
逻辑回归想解决的问题:把回归得到的结果转化为0,1的分类。上面介绍了一种粗略的解法, 用0.5做阈值,但是这样太过粗暴,不可导,不连续,求解比较困难。因此,引入sigmod函数 进行近似。
看图:
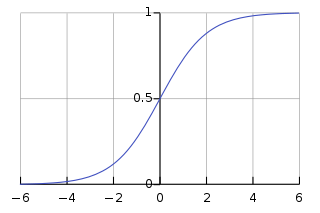
sigmod函数为: \(\theta = \frac{1}{1+e^{-z}}\)
则对于逻辑回归问题,hypothesis就是这样的形式:
\[h(x)=\frac {1}{e^{−w^Tx}}\]
那我们的目标就是求出这个预测函数h(x),使它接近目标函数f(x)。
我们令目标函数为\(f(y=+1|x)=\),则
\[ p(y|x) = \left\{ {\begin{array}{*{20}{c}} {f(x),y = + 1}\\ {1 - f(x),y = - 1} \end{array}} \right. \]
sigmod函数满足一个性质: \(h(-x)=1-h(x)\)
那么似然函数为:
\[likehood(h)=p(x_1)h(+x_1)\times p(x_2)h(-x_x) \times \cdots p(x_N)h(- x_N)\]
\(p(x_N)\)对所有的h来说都是一样的,可以忽 略,再加上log, 那么损失函数为:
\[ \mathop {\max }\limits_h = \log \prod\limits_{i = 1}^N {h({y_i}{x_i})} \]
带入\(w\),
\[ \mathop {\max }\limits_w = \log \prod\limits_{i = 1}^N {\theta({y_i}{w^T}{x_i})} \]
接着,我们将maximize问题转化为minimize问题,添加一个负号就行,并引入平均数操作\(\frac{1}{N}\):
\[ \mathop {\min }\limits_w \frac{1}{N}\sum\limits_{i = 1}^N { - \ln \theta ({y_i}{w^T}{x_i})} \]
带入\(\theta(s)=\frac{1}{1+exp(-s)}\)
得到:
\[ \mathop {\min }\limits_w \frac{1}{N}\sum\limits_{i = 1}^N {\ln (1 + \exp ( - {y_i}{w^T}{x_i}))} \]
其中\(\ln (1 + \exp ( - {y_i}{w^T}{x_i})\) 叫做交叉熵。
当然还有其他的推导方法,周志华老师书上采用另外一种推导方法(p59),
也就是:
\[ \sum_i {y_i p(y=1|x_i) + (1-y_i)p(y=0|x_i)} \]
支持向量机
支持向量机求解的是获得最大支撑面。
巴啦巴拉求解之后得到:
\[ \min_{w,b}\frac{1}{2}||w||^2 \\ s.t.\; y_i(w^Tx_i+b) \ge 1, \; i = 1,2,...,N. \]
损失函数就是:
\[ \sum_{i=1}^{N} \frac{1}{2}||w||^2 + max(0, 1-y_i(w^Tx_i+b)) \]
那SVM为什么不采用求解这个损失函数呢,因为部分不可导,求解也会失去核技巧的便利,以及svm对偶求解可以获得稀疏解,仅保存支撑向量即可。
令\(s=w^Tx+b\),
分类模型都是用连续可导函数去近似01损失函数,并且都是它的上界,图中还缺少了AdaBoost的指数损失函数\(e^{-ys}\)。

至此,线性模型介绍完毕。
